1. Pengertian
Probabilitas
Probabilitas atau Peluang adalah suatu ukuran tentang
kemungkinan suatu peristiwa (event) akan terjadi di masa mendatang.
Probabilitas dapat juga diartikan sebagai harga angka yang menunjukkan seberapa
besar kemungkinan suatu peristiwa terjadi, di antara keseluruhan
peristiwa yang mungkin terjadi. Probabilitas dilambangkan dengan P.
§ Contoh 1: Sebuah mata uang
logam mempunyai sisi dua (H & T) kalau mata uang tersebut dilambungkan satu
kali, peluang untuk keluar sisi H adalah ½.
§ Contoh 2: Sebuah dadu untuk keluar mata ‘lima’
saat pelemparan dadu tersebut satu kali adalah 1/6 (karena banyaknya permukaan
dadu adalah 6).
Rumus :
P (E) = X/N
P : Probabilitas
E : Event (Kejadian)
X : Jumlah kejadian yang
diinginkan (peristiwa)
N : Keseluruhan kejadian yang
mungkin terjadi
Walaupun cara penelitian dengan menggunakan sampling akan menimbulkan
kesimpulan dan keputusan yang melibatkan resiko kekeliruan dan ukuran
ketidakpastian, tetapi penelitian melalui sampling akan memberikan banyak
keuntungan.
Probabilitas yang rendah menunjukkan kecilnya kemungkinan suatu
peristiwa akan terjadi. Suatu probabilitas dinyatakan antara 0
sampai 1 atau dalam presentase. Probabilitas 0 menunjukkan peristiwa yang
tidak mungkin terjadi, sedangkan probabilitas 1 menunjukkan peristiwa yang
pasti terjadi.
Ada tiga hal penting dalam probabilitas, yaitu:
1. Percobaan adalah pengamatan terhadap
beberapa aktivitas atau proses yang memungkinkan timbulnya paling sedikit 2
peristiwa tanpa memperhatikan peristiwa mana yang akan terjadi.
2. Hasil adalah suatu hasil dari sebuah
percobaan.
3. Peristiwa adalah kumpulan dari satu atau
lebih hasil yang terjadi pada sebuah percobaan atau kegiatan.
2. Manfaat Probabilitas
dalam Peneitian
Manfaat probabilitas dalam kehidupan sehari-hari adalah membantu kita dalam
mengambil suatu keputusan, serta meramalkan kejadian yang mungkin terjadi. Jika
kita tinjau pada saat kita melakukan penelitian, probabilitas memiliki beberapa
fungsi antara lain:
§ - Membantu peneliti
dalam pengambilan keputusan yang lebih tepat.
§ -Dengan teori
probabilitas kita dapat menarik kesimpulan secara tepat atas hipotesis yang
terkait tentang karakteristik populasi.
§ - Mengukur derajat
ketidakpastian dari analisis sampel hasil penelitian dari suatu
populasi.
3. Pendekatan
Probabilitas
Ada 3 (tiga) pendekatan konsep untuk mendefinisikan probabilitas dan
menentukan nilai-nilai probabilitas, yaitu :
a) Pendekatan Klasik,
b) Pendekatan Frekuensi
Relatif, dan
c) Pendekatan Subyektif.
1)
Pendekatan Klasik
Pendekatan klasik didasarkan pada sebuah peristiwa mempunyai kesempatan
untuk terjadi sama besar (equally likely). Probabilitas suatu peristiwa
kemudian dinyatakan sebagai suatu rasio antara jumlah kemungkinan hasil dengan
total kemungkinan hasil (rasio peristiwa terhadap hasil).
Probabilitas suatu peristiwa = Jumlah
kemungkinan hasil / Jumlah total kemungkinan hasil
Jika ada a kemungkinan yang dapat terjadi pada kejadian A dan ada b
kemungkinan yang dapat terjadi pada kejadian A, serta masing-masing kejadian
mempunyai kesempatan yang sama dan saling asing, maka probabilitas/peluang
bahwa akan terjadi a adalah:
P (A) = a/a+b ; dan peluang bahwa akan
terjadi b adalah: P (A) = b/a+b
Contoh:
Pelamar pekerjaan
terdiri dari 10 orang pria (A) dan 15 orang wanita (B). Jika yang diterima
hanya 1, berapa peluang bahwa ia merupakan wanita?
Jawab:
P (A) = 15/10+15 = 3/5
2)
Pendekatan Relatif
Besarnya probabilitas suatu peristiwa tidak dianggap sama, tetapi
tergantung pada berapa banyak suatu peristiwa terjadi dari keseluruhan
percobaan atau kegiatan yang dilakukan. probabilitas dapat dinyatakan sebagai
berikut :
Probabilitas kejadian relatif = Jumlah
peristiwa yang terjadi / Jumlah total percobaan atau kegiatan
Jika pada data
sebanyak N terdapat a kejadian yang bersifat A, maka probabilitas/peluang akan
terjadi A untuk N data adalah: P (A) = a/N
Contoh:
Dari hasil penelitian
diketahui bahwa 5 orang karyawan akan terserang flu pada musim dingin. Apabila
lokakarya diadakan di Puncak, berapa probabilitas terjadi 1 orang sakit flu
dari 400 orang karyawan yang ikut serta?
Jawab:
P (A) = 5/400 = P (A)
= 1/80
3)
Pendekatan Subjektif
Besarnya suatu
probabilitas didasarkan pada penilaian pribadi dan dinyatakan dalam derajat
kepercayaan. Penilaian subjektif diberikan terlalu sedikit atau tidak ada
informasi yang diperoleh dan berdasarkan keyakinan.
4. Konsep Dasar dan Hukum
Probabilitas
Dalam mempelajari hukum dasar probabilitas berturut-turut akan dibahas
hukum penjumlahan dan hukum perkalian.
1) Hukum Penjumlahan
Hukum penjumlahan
menghendaki peristiwa saling lepas (mutually exclusive) dan peristiwa/kejadian
bersama (non mutually exclusive).
§
Saling meniadakan (mutually exclusive)
Apabila suatu peristiwa terjadi, maka peristiwa lain tidak dapat terjadi
pada saat bersamaan.
Rumus penjumlahan untuk kejadian-kejadian yang saling meniadakan:
Rumus penjumlahan untuk kejadian-kejadian yang saling meniadakan:
P (A U B) = P (A atau B)= P (A) + P (B)
Contoh:
Probabilitas untuk
keluar mata 2 atau mata 5 pada pelemparan satu kali sebuah dadu adalah:
P(2 U 5) = P (2) + P
(5) = 1/6 + 1/6 = 2/6
§
Kejadian Bersama (Non Mutually Exclusive)
Peristiwa Non Mutually Exclusive (Joint) dua peristiwa
atau lebih dapat terjadi bersama-sama (tetapi tidak selalu bersama).
Rumus penjumlahan untuk kejadian-kejadian yang tidak saling meniadakan:
Rumus penjumlahan untuk kejadian-kejadian yang tidak saling meniadakan:
Dua Kejadian
P (A U B) =P(A) + P (B) – P(A ∩ B)
Tiga Kejadian
P(A U B U C) = P(A) + P(B) +
P(C) – P(A ∩ B) – P(A ∩ C) – P(B ∩ C) + P(A ∩ B ∩ C)
Peristiwa terjadinya A
dan B merupakan gabungan antara peristiwa A dan peristiwa B. Akan tetapi
karena ada elemen yang sama dalam peristiwa A dan B, Gabungan peristiwa A
dan B perlu dikurangi peristiwa di mana A dan B memiliki elemen yang sama.
Dengan demikian, probabilitas pada keadaan di mana terdapat elemen
yang sama antara peristiwa A dan B maka probabilitas A atau B adalah
probabilitas A ditambah probabilitas B dan dikurangi probabilitas elemen
yang sama dalam peristiwa A dan B.
§
Peristiwa Pelengkap (Complementary Event)
Apabila peristiwa A dan B saling melengkapi, sehingga jika peristiwa A
tidak terjadi, maka peristiwa B pasti terjadi. Peristiwa A dan B dikatakan
sebagai peristiwa komplemen.
Rumus untuk kejadian-kejadian yang saling melengkapi :
Rumus untuk kejadian-kejadian yang saling melengkapi :
P(A)+P(B) = 1 atau P(A) = 1 – P(B)
2)
Hukum Perkalian
§
Hukum Bebas (independent)
Hukum perkalian menghendaki setiap peristiwa adalah independen,
yaitu suatu peristiwa terjadi tanpa harus menghalangi peristiwa lain
terjadi. Peristiwa A dan B independen, apabila peristiwa A terjadi tidak
menghalangi terjadinya peristiwa B.
P(A ∩ B) = P (A dan B) = P(A) x P(B)
Contoh soal 1:
Sebuah dadu
dilambungkan dua kali, peluang keluarnya mata 5 untuk kedua kalinya adalah:
P (5 ∩ 5) = 1/6 x 1/6
= 1/36
Contoh soal 2:
Sebuah dadu dan koin
dilambungkan bersama-sama, peluang keluarnya hasil lambungan berupa sisi H pada
koin dan sisi 3 pada dadu adalah:
P (H) = ½, P (3) = 1/6
P (H ∩ 3) = ½ x 1/6 =
1/12
§
Peristiwa Bersyarat (Tidak Bebas) / (Conditional Probability)
Probabilitas bersyarat adalah probabilitas suatu peristiwa akan terjadi
dengan ketentuan peristiwa yang lain telah terjadi. Peristiwa B terjadi dengan
syarat peristiwa A telah terjadi.
P(A dan B) = P(A x P(B|A) atau P(B dan
A) = P(B) x P(A|B)
Contoh :
Dua kartu ditarik dari
satu set kartu bridge, peluang untuk yang tertarik keduanya kartu as adalah
sebagai berikut: Peluang as I adalah 4/52 -> P (as I) = 4/52
Peluang as II dengan
syarat as I sudah tertarik adalah 3/51
P (as II │as I) = 3/51
P (as I ∩ as II) = P
(as I) x P (as II│ as I) = 4/52 x 3/51 = 12/2652 =1/221
5. Diagram Pohon
Probabilitas
Diagram pohon merupakan suatu
diagram yang menyerupai pohon dimulai dari batang kemudian menuju ranting dan
daun. diagram pohon dimaksudkan untuk membantu menggambarkan probabilitas atau
probabilitas bersyarat dan probabilitas bersama. diagram pohon sangat berguna
untuk menganalisis keputusan-keputusan bisnis dimana terdapat tahapan-tahapan
pekerjaan.
Contoh:
1)
Ruang Sampel dan Titik Sampel
Ruang sampel adalah
himpunan dari semua hasil yang mungkin pada suatu
percobaan/kejadian. Ruang Sampel suatu percobaan dapat dinyatakan dalam
bentuk diagram pohon atau tabel.
Titik Sampel adalah
anggota-anggota dari ruang sampel atau kemungkinan-kemungkinan yang muncul.
Contoh:
Pada percobaan
melempar dua buah mata uang logam (koin) homogen yang berisi angka (A) dan
gambar (G) sebanyak satu kali. Tentukan ruang sampel percobaan tersebut.
1. Dengan Diagram Pohon
Kejadian yang mungkin:
AA : Muncul sisi angka
pada kedua koin
AG : Muncul sisi angka
pada koin 1 dan sisi gambar pada koin 2
Dengan Tabel
Ruang sampel = {(A,A),
(A,G), (G,A), (G,G)}
Banyak titik sampel ada 4 yaitu (A,A), (A,G), (G,A), dan (G,G)
Teorema
Bayes
Dalam teori
probabilitas dan statistika, teorema Bayes adalah sebuah teorema
dengan dua penafsiran berbeda. Dalam penafsiran Bayes, teorema ini
menyatakan seberapa jauh derajat kepercayaan subjektif harus berubah secara
rasional ketika ada petunjuk baru. Dalam penafsiran frekuentis teorema
ini menjelaskan representasi invers probabilitas dua kejadian. Teorema ini
merupakan dasar dari statistika Bayes dan memiliki penerapan dalam sains,
rekayasa, ilmu ekonomi (terutama ilmu ekonomi mikro), teori permainan,
kedokteran dan hukum. Penerapan teorema Bayes untuk memperbarui kepercayaan
dinamakan inferens Bayes.
atau
Prinsip
Menghitung
1. Faktorial
Faktorial digunakan untuk mengetahui berapa banyak cara yang mungkin dalam mengatur sesuatu. Hasil perkalian semua bilangan bulat positif secara berurutan dari 1 sampai dengan n disebut n faktorial. Dari definisi faktorial tersebut, maka dapat dituliskan prinsip menghitung faktorial sebagai berikut :
Faktorial digunakan untuk mengetahui berapa banyak cara yang mungkin dalam mengatur sesuatu. Hasil perkalian semua bilangan bulat positif secara berurutan dari 1 sampai dengan n disebut n faktorial. Dari definisi faktorial tersebut, maka dapat dituliskan prinsip menghitung faktorial sebagai berikut :
n ! = n x (n-1) x (n-2) x (n-3) x …
3 x 2 x 1
n ! dibaca n faktorial
nb: 0! = 1dan 1! = 1
Contoh:
3! = 3 x 2 x
1 = 6
5! = 5 x 4 x 3 x 2 x 1 = 120
5! = 5 x 4 x 3 x 2 x 1 = 120
2. Permutasi
Permutasi digunakan untuk mengetahui jumlah kemungkinan susunan (arrangement) jika terdapat satu kelompok objek. pada permutasi berkepentingan dengan susunan atau urutan dari objek. Permutasi dirumuskan sebagai berikut :
Permutasi digunakan untuk mengetahui jumlah kemungkinan susunan (arrangement) jika terdapat satu kelompok objek. pada permutasi berkepentingan dengan susunan atau urutan dari objek. Permutasi dirumuskan sebagai berikut :
atau
dimana :
P = Jumlah
permutasi atau cara objek disusun
n = jumlah total objek yang disusun
r/k = jumlah objek yang digunakan pada saat bersamaan, jumlah r/k dapat sama dengan n atau lebih kecil
n = jumlah total objek yang disusun
r/k = jumlah objek yang digunakan pada saat bersamaan, jumlah r/k dapat sama dengan n atau lebih kecil
! = tanda
dari faktorial
Contoh:
Di kantor
pusat DJBC Ada 3 orang staff yang dicalonkan untuk menjadi mengisi kekosongan 2
kursi pejabat eselon IV. Tentukan banyak cara yang bisa dipakai untuk mengisi
jabatan tersebut?
Jawab : Permutasi P (3,2), dengan n =3 (banyaknya staff) dan
k =2 (jumlah posisi yang akan diisi)
Permutasi Unsur-unsur yang sama
Contoh:
Tentukan
permutasi atas semua unsur yang dibuat dari kata MATEMATIKA!
Jawab: Pada kata MATEMATIKA terdapat 2 buah M, 3 buah A,
dan 2 buah T yang sama, sehingga permutasinya adalah:
Permutasi Siklis
RUMUS:
banyaknya permutasi = (n-1)!
Contoh:
Suatu
keluarga yang terdiri atas 6 orang duduk mengelilingi sebuah meja makan yang
berbentuk lingkaran. Berapa banyak cara agar mereka dapat duduk mengelilingi
meja makan dengan cara yang berbeda?
Jawab : Banyaknya cara agar 6 orang dapat duduk mengelilingi
meja makan dengan urutan yang berbeda sama dengan banyak permutasi siklis
(melingkar) 6 unsur yaitu :
3. Kombinasi
Kombinasi
digunakan apabila ingin mengetahui berapa cara sesuatu diambil dari keseluruhan
objek tanpa memperhatikan urutannya. Jumlah kombinasi dirumuskan sebagai
berikut :
Contoh:
Saat akan
menjamu Bayern Munchen di Allianz arena, Antonio Conte (Pelatih Juventus) punya
20 pemain yang akan dipilih 11 diantaranya untuk jadi starter. Berapa banyak
cara pemilihan starter tim juventus? (tidak memperhatikan posisi pemain).









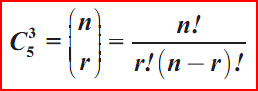

Tidak ada komentar:
Posting Komentar